2021年の個人的ゴールデンウィークの課題図書、『フェルマーの最終定理』を読み切りました!
文字がみっちり詰まって500ページ級というボリューム。タイトルから溢れる数学的難解な雰囲気。読む前には挫折するかと思いましたが、内容は素晴らしくドラマチック。この本は超おススメなので、是非多くの方に読んで欲しいです。
書き手であるサイモン・シン氏を調べてみると作家としてとても評価されているようでした。
難しい数学の話について、つらつらと書かれているのではなく、ドキュメント仕立てで構成されています。丁寧な取材に基づいて、フェルマーの最終定理が解き明かされるまでの背景から、当事者となるフェルマーとアンドリュー・ワイルズの人物形成までしっかりと描かれていて、最後に証明という形に結びつく。そもそもドキュメント番組の企画だったらしいので、そりゃそうか。
17世紀にピエール・ド・フェルマーが残した世界一有名な命題が、どのように生まれ、後世の人たちがどのように挑んでいったかを、ピュタゴラス(僕が中学生のころはピタゴラス表記だった気がするけど)の時代から1994年にアンドリュー・ワイルズによってされるまでの人間ドラマ、そして数学についても素人を突き放さないよう、やさしい解説も差し込みながら、素人の読み手に最後まで読ませるものになっている。
難しいことは理解してないけど、学んだことは多かった。
フェルマーの最終定理の証明は、ワイルズは一人で解いたけど、それまでの多くの先人たちのアプローチがあってこそ結実したものだし、結局一番最後はワイルズも一人ではなかった。
ドキュメンタリー動画を探したけど、見つからないな〜。要約だとなんとも味気ない。この本は傑作の部類に入ると思う。手に取ると読めるかどうか不安でいっぱいになりますが、ぜひ読み進めてみてください。全然眠くならないで読み切れます!

本の概要と要約

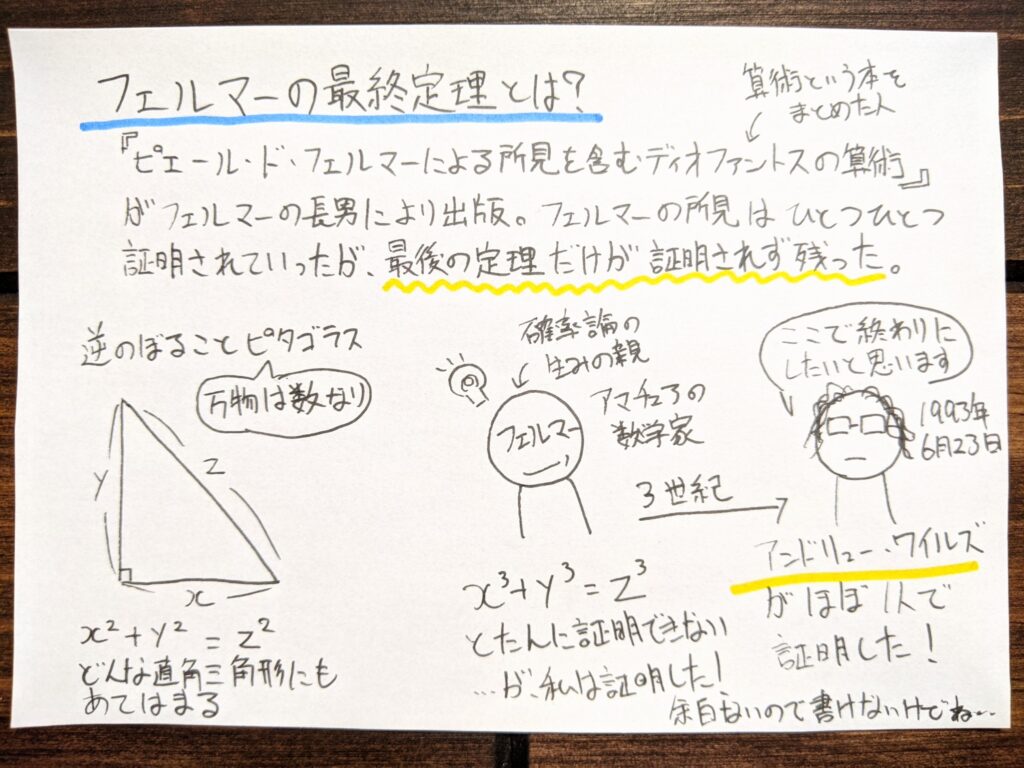


●フェルマーの最終定理
・「nが2より大きいとき、x^n + y^n = z^n が自然数解をもたないことを証明せよ」という命題
・誰もが理解できる問いなのに、300年も証明できはかった
・フェルマーの所見のひとつひとつが証明されるなか、最後に残った定理
・ルーツはピタゴラスまで遡る
・ピタゴラスの定理「x^2+y^2=z^2」という数式は、どんな直角三角形も無限にあてはまる
・フェルマーは2以外を当てはめるととたんに解が得られないことを閃いた。
・ディオファントスの算術の余白に「私はこの命題の驚くべき証明をもっている」と書き残す
・ここから3世紀に及ぶ数学者の戦いが始まる
・1993年(最終的には1994年)アンドリュー・ワイルズによって証明された
●ピエール・ド・フェルマーとは
・公務員
・アマチュアの数学者
・確率論の生みの親
●アンドリュー・ワイルズとは
・フェルマーの最終定理を証明した
・子供のころにフェルマーの最終定理に出会った
・大学院に進んでからもフェルマーの最終定理への意欲は消えなかった
・数学は科学と違い特許なく協力することが普通だったが、単独で研究した
・カムフラージュするために表面的には別の研究論文を発表していた
●挑戦の歴史
・個別のnでの証明
ーn=4はフェルマーが残していた
ーn=3はオイラーが虚数を用いて証明
ーその後も5,7が証明される
ーラメ、コーシーが解けると宣言するがクンマーにより否定
・懸賞金
ードイツ資本家ヴォルフスケールがクンマーの穴に気づく
ー遺産をフェルマーの最終定理にかける
ー数学者ほすでに関心を抱かなかった
ーパズル人気あいまりアマチュアが多数参加
・パラドックス
ーラッセルのパラドックス
ー嘘つきのパラドックス
ーゲーデルの不完全性定理
ー「この命題は証明できない」は真か偽か
ー真でも偽でも矛盾してしまう
・コンピュータ
ーチューリングが暗号解読を機械で計算
ーコンピュータにより膨大な計算が可能に
ーしかし無限に続くことは証明できない
・影響したアプローチ
ーガロアの五次方程式
ー群論という概念
ーフェルマーを帰納法で解く第1段階に使用
ー谷山=志村予想
ー楕円方程式とモジュラー形式は無限の対称性を持つ
ーフライ
ーフェルマーの最終定理に解があるなら楕円方程式になる
ー谷山=志村予想が証明できれば、フェルマーの最終定理は証明できる
ー岩澤理論
ー楕円方程式を分析する手段
ーコリヴァギン・フラッハ法
ー楕円方程式の分析に関する論文
●講演
・モジュラー形式、楕円曲線、ガロア表現というケンブリッジでの全3回にわたる講演
・噂が広まり最後は人で溢れる
・「ここで終わりにしたいと思います」で締めくくり拍手喝采
●最後の試練
・論文のレフェリーがミスを発見
・修整どころが欠陥とみられた
・1度失敗した岩澤理論で補うことに成功
・発表から14ヶ月経って、ようやく正式に発表された
著者:サイモン・シン
サイモン・シンはイングランド出身のTV番組のプロデューサーでサイエンス・ライター。ケンブリッジ大学大学院で素粒子物理学の博士号を取得。 テレビ局BBCに就職し、ドキュメンタリー番組『フェルマーの最終定理――ホライズンシリーズ』(96年)で、国内外で多数の賞を受賞。以降も『暗号解読』『宇宙創成』といったサイエンス系の著書が評価を得ている。
●インタビュー記事
サイモン・シン インタビュー 「数十年来の陰謀を暴く」『数学者たちの楽園』刊行記念(『波』2016年6月号 掲載)
●SNS
Twitter:@SLSingh
本の解説と感想
フェルマーの最終定理とは

上記にまとめた通り、フェルマーの最終定理とは、「nが2より大きいとき、x^n + y^n = z^n が自然数解をもたない」というものであり、ピエール・ド・フェルマーはこの証明を持っていると書き残しただけで、その証明は彼の頭の中だけにあり、挑戦状のような形で残されました。
とてもシンプルなので、数学が苦手な人だとしても、これを証明せよという命題の意味は容易く理解できます。そしてn=2はピュタゴラスの定理という奇跡の数式。それにも関わらず、n=3以上になったとき、解が全く得られないなんていうことがあるのか。そのギャップによって、世界一有名な数学の問題として3世紀の長きに渡って、数学者たちが挑戦してきたのです。
起源はピュタゴラスの定理まで遡る
「ピュタゴラスの定理」と言えば、どんなに数学に縁のない人でも、聞いたことがありますよね。○○の定理のなかで一番簡単で冷静に考えると革命的で数学の美を象徴するようなあの数式です。
直角三角形の斜辺の2乗は他の二辺の2乗の和に等しい
『フェルマーの最終定理』p37

この数式のすごさは、nがどんな数字だろうと当てはまるということです。わたし、上の図をパワーポイントで自作したのですが、この直角三角形ってピュタゴラスの定理がなかったら作れないですからね。
さて、そんな偉人ピュタゴラスは紀元前6世紀に生きた人。世界を旅して数学の規則を全て身につけたのだとか。そんなピュタゴラスがどのように生きたかも、本書には書いてあります。このピュタゴラスの功績がなければ、そもそもフェルマーの最終定理が存在しないというところが、ドラマ性を生んでいる一つの要素です。
現代に生きる我々であれば、誰もが知るピュタゴラスですが、最初は少年を金で釣って弟子にしたそうです。孤独を楽しむつもりで宮廷から誘いを受けたらしいのですが、結局寂しさには耐えられず、教えるということをやったようです。
そうしているうちに学問所のようなものを設立したようですが、政治的に受け入れられず、場所を変え、やがてミロンという富豪で怪力を持つ男にパトロンになってもらったそうです。やがて、弟子も600人ほどとなり、ピュタゴラス教団を設立します。
ピュタゴラス教団は「完全数」という自然数を崇拝しました。完全数とは、例えば「6」で、1+2+3=6となるような、自分自身を除く正の約数の和に等しくなる自然数のことです。
これによって、教団は、宇宙の霊的神秘が明らかになり神々に近づけると信じました。事実上、宗教です。それが示されるのが、ピュタゴラスの哲学。
万物は数なり
『フェルマーの最終定理』p48
実際に自然現象支配する数学規則を初めて明らかにしていきます。そのひとつが和音。
どんな自然現象でも数がひょっこり顔を出すことが分かってきたのです。ピュタゴラスは、音楽の和音から惑星の軌道に至るまで、あらゆる事柄の背後に数が潜んでいることに気づき「万物は数なり」と言い切るまでになったのです。
で、そこにきてピュタゴラスの定理です。
「直角三角形の斜辺の二乗は他の2辺の二乗の和に等しい」というのは、実は中国人やバビロニア人も利用していたものの、「すべて」の直角三角形で成り立つことは知られていなかったのです。この定理が普遍的に成り立つことを初めて示したのがピュタゴラスだったのです。
ピエール・ド・フェルマーと余白
フェルマーは、誰にも解が見つけられないのは解が存在しないからだという驚くべき主張をしたのだった
『フェルマーの最終定理』p71
「フェルマーの最終定理」という挑戦状を後世に残した、ピエール・ド・フェルマーその人について少しまとめます。
フェルマーは、1601年にフランスで生まれました。「ド」とつく名前からも分かる通り、家柄は悪くなく、役人として身を立てる道を進んでいきます。一方で数学の問題を解くのが好きで、後世「アマチュアの数学家」の一番手として評されます。
フェルマーはなかなか、やっかいな人だったらしく、フェルマーが証明したさまざまな問題を、公表するように勧められても、拒んだそうです。公表したからと言って、得になることがなかったからです。
フェルマーにとって証明を公表しても何の意味もなかったのです。
数学者たちの間でも有名だったらしいのですが、フェルマーの最終定理について解が得られない数学者はイライラを募らせ、デカルトからは「大法螺吹き」と呼ばれ、ポリスは「いまいましいフランス人」と罵ったそう。
数学の証明は、公表すれば聞きかじりの初心者までもが寄ってたかって難癖をつけたがるあら探しが発生するもの。フェルマーはそういった、煩わしさを持たないようあえて発表しなかったのだろうと推測されています。
ちなみにフェルマーは、パスカルとともに力を合わせて確率論における最初の証明を発見した人でもあります。プロギャンブラーから、「途中で中止することになったギャンブルの賞金をどうするか」という問題をパスカルに尋ねたのが発端。
起こりうるゲームの結末を数え上げ、それぞれの結末が起こる確率を各対戦者に振り分ければ良いことに気がついた
『フェルマーの最終定理』p88
こんなフェルマーに影響を与えたのが、ディオファントスの『算術』という著書です。この大著にも歴史があり、詳しくは本書をぜひ読んで欲しいです。
ディオファントスが『算術』という本を書いたのは3世紀。
ギリシャ語版は13巻でしたが、アレクサンドリアが外国の軍隊の脅威にさらされ、カエサルがアレクサンドリアの艦隊に火を放ったとき、港のそばにあった図書館にあった百数十万巻の書物が被害を受け、算術も6巻のみが残るという状況。これが16世紀に入ってようやくラテン語訳が刊行されました。
このラテン語訳版に、フェルマーは出会います。
フェルマーは、ディオファントスの『算術』から先人たちの数学の知識を得て、ピタゴラスらが構築した数の学問に触れました。
フェルマーは多くの問題を解きましたが、ディオファントスと大きく違ったのは、後世のために残そうとしなかった点です。ディオファントスの『算術』は教科書、マニュアルなのに対し、フェルマーが残したのはメモ。解法を発見したとき、走り書きをして、そのままくず入れに放り込むこともあったのだとか。
後世にとって幸運だったのは、ラテン語訳の『算術』には各ページに十分な余白があり、フェルマーはその余白に論法やコメントを書き込んでいたのです。そしてその『算術』の余白に書き込まれたものの一つがのちに「フェルマーの最終定理」と呼ばれる命題をとなります。
フェルマーの死後、長男がフェルマーの残した算術を『ピエール・ド・フェルマーによる所見を含むディオファントスの算術』という形で出版。所見の多くが解かれていったものの、最後の最後に残ったものがフェルマーの最終定理と呼ばれ、数学者たちを悩ませ、数学最大の謎という伝説になったのです。
フェルマーが解けるものなら解いてみろ、という思わせぶりな書き込みが多くの数学者を夢中にさせたのかもしれません。それがこのメモです。
私はこの命題の真に驚くべき証明をもっているが、余白が狭すぎるのでここに記すことはできない
『フェルマーの最終定理』p118
証明への挑戦の歴史
フェルマーの最終定理の証明は、そのものに挑んだ人たちもいれば、フェルマーの最終定理を解こうと思ってはいなかったけど、解くための重要な考え方が全く別のアプローチから登場したり、ドラマ性がかなりあります。
おおよその流れは、
・すぐに解けるはずだろ…
・nを限定してであれば徐々に解けてきた(でも全然進んでない)
・無限のnの証明ってできないんじゃない?(雲行きが怪しくなる)
・役に立つかもわからない証明に学者人生の時間を使うのにはもったいない
・懸賞金なども出て、クイズブームでアマチュア参戦
・ひそかに情熱を燃やしたものだけが研究する
という感じでしょうか。
フェルマーの最終定理のポイントは
・nが無限続く場合に解きがたい
・証明しても何も役に立たないのではないかという疑念
というところだったのではないかなと思います。
特に、序盤は早々に解けるんじゃないかという期待を抱かせるものがあったのではないかと思います。なぜなら、n=4のときの証明はフェルマーが別の部分のメモで残していたもので証明されていたのです。
で、オイラー(この人もまた偉大な数学者のひとり)が、フェルマーの残したメモをヒントにn=3の場合を証明することができました。
ここから歩みが遅いのですが、だんだんとn=5のとき、n=7のとき、と一つ一つの数の場合に証明がなされていったのですが、一向に「どこまでも無限に続く数」での証明ができません。解けると宣言した学者が二人いたのですが、彼らのアプローチ方法に穴があると、クンマーという人物が発表することで一気にトーンダウンしてしまいます。
あまりに解けないことと、研究するにしても膨大な時間を費やさなければならないことで、やがて、数学者からは関心が無くなっていきます。
しかし、フェルマーの最終定理が世間への息を吹き返すことになります。それが懸賞金です。
懸賞金がかけられたエピソードもまた面白い。
ドイツ資本家ヴォルフスケールが、意中の人に振られて自殺しようとして家を整理していたときにぼんやりと読んだクンマーの論文に穴があることを発見します。これに喜びを見出したヴォルフスケールは、まだフェルマーの最終定理が解ける可能性があると考え、それに気が付いた自分に嬉しくなって自殺を辞め、遺言書にフェルマーの最終定理を証明したものに遺産を分けると残します。
これが話題を呼び、多くのアマチュアの関心を引きました。しかし、やはり素人には解けない。この後も学者からは否定的な見解が出ます。それがゲーデルの不完全性定理。
「この命題は証明できない」という命題に対して、真でも偽でも矛盾が生じるというものです。
真のとき、証明ができないということなのに、証明ができてしまっている。
偽のとき、証明ができるということなのに、「証明できない」と命題に書かれている。
なんかこじつけな気がしなくもないですが、とにかく矛盾して「決定不可能」状態です。
フェルマーの最終定理も決定不可能であり、そういう考えにすれば、フェルマーからの挑戦状は解決してしまうというのもまた、事実としてあるわけです。
ところで、学者の世界の外で環境に大きな変化が現れます。戦争です。戦争はいつの時代もテクノロジーの進化を促します。数学、科学界に大いに貢献することになるものの一つに、暗号解読のために計算機の登場があります。
第2次世界大戦のとき、イギリスのアラン・チューリングは暗号解読を機械で計算するものを開発します。ドイツの暗号生成器エニグマの解明のために用いられましたが、今日のコンピュータの源流であり、コンピュータは人間が障害をかけても計算できない膨大な計算を自動で短時間に計算することを可能としました。
フェルマーの最終定理も、コンピュータのおかげで、1980年代にはn=25,000まで証明を成し遂げたらしいのですが、いくら個々のnが証明できても無限に続くことは証明できなかったのです。
アンドリュー・ワイルズという人
「フェルマーの最終定理」を証明した人物、それがアンドリュー・ワイルズです。
彼が幼いころ惹きつけられたのが、E.T.ベルの『最後の問題』という本でした。この本には、ピタゴラスの定理が説明されていました。
「x^2+y^2=z^2」というピュタゴラスの定理は、この三つ組み数が無数に存在することが述べられているのに、どうやら全てを三乗にすると似たような式なのに整数解が全く求まらなくなるらしい。何世代にもわたって当てはまる数を見つけることができていない。
ベルの本を読むと、フェルマーがピュタゴラスの研究に惹かれ、少しだけ変形した「x^3 + y^3 = z^3」の方程式を研究するなったいきさつを知り、そしてフェルマーが「nが2より大きいとき、x^n + y^n = z^n が自然数解をもたない」ということの証明は、世界中の数学者が永遠の時をかけても見つけられないと豪語し、しかも自分だけは答えを知っているというのです。
アンドリュー・ワイルズはこうしてフェルマーの最終定理の虜となったのです。
ワイルズが研究を始めてからは、一人でこの問題に取り組んだそうです。数学の世界では、コミュニティというのが重要な役割を果たすのだそうです。一人だけで解くのではなく、仲間の意見なども参考に解いていくのが一般的なのだとか。
というのも、特許が絡むものではなく、自由にアイデアを交換し合うもので、隠す必要がないというのが最大の理由。しかしワイルズは一人での研究を選択します。
それは、
・アイデアを盗まれることなく栄光を手にしたかったから
・公にさらされることで突っ込みがはいるなど集中できなくなるから
という理由だったようです。
大学院に入ってからも、フェルマーの最終定理を研究したかったものの、それを封印します。
指導者であったジョン・コーツは、ワイルズのために楕円曲線論と呼ばれる分野の研究を薦めます。これがワイルドにとって重大な転機となり、フェルマーの最終定理に挑むための新たな手法を彼に与えることになるのですが、のちほど説明します。
時は流れ、1993年6月23日ケンブリッジの数学の講演で、初めて、突然にワイルズの研究結果が発表されるのです。
ついに「フェルマーの最終定理」証明へ
ここで終わりにしたいと思います
『フェルマーの最終定理』p75
ワイルズの挑戦
ワイルズの発想のなかで、私が一番納得と共感をしたのは、「フェルマーが証明した時代の知識だけで、フェルマーの最終定理が証明ができるはず」という仮説でした。その原点に立てば、最新の理論などなくとも解明できるはずなのです。
しかしながら、ワイルズが証明したフェルマーの最終定理の解法は、フェルマー以降の研究がなければたどり着けないものでした。なのでもしかしたらフェルマーが証明を持っていると言っていたのは、嘘かもしれないし、誤りがあったかもしれないのです。(現在でもワイルズの解法ではなく、フェルマーの解法を研究している方もいるようです)
ワイルズが証明の出発点にしたのは、帰納法。帰納法であれば、一つの場合を証明するだけで、無限にある全ての場合を証明することが可能になるからです。
この第一段階のヒントとなったのが、ガロアの5次方程式。(もう私自身、何を言っているか分かりません…)。このガロアという人も数奇な運命を辿っていたりします。関係者ごとに人を感じることができるのがこのサイモン・シン著の『フェルマーの最終定理』の面白いところです。
ガロアは5次方程式の論文を審査委員会に提出したのですが、それが政治的な意図で届かなかったらしく、反乱軍に入隊して逮捕されます。もうすぐ解放されるというところで、決闘を迫られ命を落とします。遺書とも言えるメモの中に5次方程式を書き残そうとしており、ワイルズはこのなかの「群論」という概念を、証明に利用します。
こうして、ワイルズが研究を進めるなか、突然「フェルマーの最終定理が解けた」という報道が巡ります。東京都立大学の数学者・宮岡洋一が、微分幾何学という全く異なる角度からこの問題にアプローチしていたのです。しかし、この証明は途中で矛盾が指摘され、問題は解消されず証明は失敗に終わってしまいます。
さぞかしワイルズの心はざわついたでしょう。
ワイルズのほうは、忍耐が続きます。岩澤理論と呼ばれる方法を調べたて活用を模索したものの、そのアプローチにも敗れてしまいます。そんななか、かつてワイルズを指導したジョン・コーツが、そのとき指導していたマテウス・フラッハという学生が楕円方程式を分析する素晴らしい論文を書いていると教えてくれます。これは大きな駆動になると考え、ワイルズは、この学生の分析をもとにした、コリヴァギン・フラッハ法を拡張することにしました。
そして海の向こうでは、のちにフェルマーの最終定理に重要に結びつく研究がなされていました。
谷山=志村予想
ここで二人の日本人が突如としてフェルマーの最終定理の証明に関わってきます。。谷山豊と志村五郎という数学者が、楕円方程式とフェルマーの最終定理とを分かちがたく結びついてる一連の重要な出来事の引き金を引いていました。それが、谷山=志村予想です。(内容は、わたしの至らない脳では解説できないので全く期待しないでください…)
モジュラー形式というのは、対称性をもつ上半平面上の複素解析的函数で…と、詳しくは画像検索して頂いたほうが良いかと思います。
このモジュラー形式というのは、信じられないほど高い対称性を持っているということがわかり、それが無限の対称性を持つというとうことがわかってきました。そして、楕円方程式がどれかの無限に続くモジュラー形式と関連しているに違いないというのが二人の予想でした。(予想というのは証明されていないけど、ほぼそうだよねと暗黙に了承されているもの
さらに、1984年秋、ドイツ数学者フライが、「谷山=志村予想を証明する事は、そのままフェルマーの最終定理の証明に繋がる」という驚くべき主張をしました。このフライって人の登場は、本を読み進めて後半に入っていくうちに、証明できないだろこれ…っていう雰囲気が漂うところ、急にまだいけるんじゃないか!?という空気にしてくれます。期待を落としてから戻す、物語の真骨頂。盛り上がって参りました。
そのフライという人物、フェルマーの最終定理の解が存在すると仮定したときに、数式を並べ替えると、そのまま楕円方程式であることを示したのです。しかしこれは異常な性質を持っているとも同時に指摘しました。
谷山=志村予想はすべてのモジュラーが楕円方程式でなければならなのに、フライが示した楕円方程式は極めて異常なのでモジュラーではあり得ない。つまり、フライの方程式が成り立たないのであれば、フェルマーの最終定理は解がない、ということになるので、フェルマーの最終定理が成り立つことになります。
…うん。理解できているかはだいぶ怪しい。
まあ、とにかくフライという人は、フェルマーの最終定理の審議が谷山志村予想が証明できるかどうかにかかっているというドラマティックな結論を導いたんです。
1993年6月23日ケンブリッジ
アンドリュー・ワイルズは、これまで密かにフェルマーの最終定理の研究をしてきましたが、そのときに証明に使おうとしていることがこの1年で見出された手法に頼りすぎていることに懸念を抱き、自分一人でやり遂げることに限界を感じ、ニック・カッツという人物にコリヴァギン・フラッハ法を進展させたいと頼み込みます。
結果、7年ものあいだ一心に努力した末に、ワイルズはついに谷山志村予想の証明を完成させたのです。つまりそれは、フェルマーの最終定理が証明されたことを意味します。
1993年6月21日から23日にかけ、ワイルズの講演は3日にわけ行われました。
タイトルは、「モジュラー形式、楕円曲線、ガロア表現」。数学者が見ても、それがフェルマーの最終定理を証明する内容だとは一目では気が付くことができないものでした。
1日目が始まる前に、数学者の間ではフェルマーの最終定理を証明したという噂が出回ります。
1日目の講演が終わり、また噂を聞きつけて人が集まり2回目の講演では大幅に聴衆が増えます。ワイルズは谷山志村予想をほのめかす計算をして見せて聴衆を焦らせます。3回目の講演では、ワイルズの証明を支える理論を生み出した人たちがほとんど全員その場に揃っていましたそうです。
そして、証明が完了し、フェルマーの最終定理を黒板に書き、「ここで終わりにしたいと思います」という言葉を発すると、聴衆の拍手喝采でその瞬間を過ごしました。
あれほど見事なアイディアに溢れ、ドラマティックな緊張感をもち、みごとに構築された講演は見たことがありません。
『フェルマーの最終定理』p380
さらなる苦難
拍手喝采で講演が終わり、ワイルズの論文は審査に入ることになります。ここから想像を絶する苦難が待ち受けていました。
ミスと言えるものが発見されたのです。
ワイルズはこれをすぐに修正することができませんでした。フェルマーの最終定理の証明が正式に発表されないことに数学会はざわつきます。誰もが諦めかけました。ワイルズ本人も。
このときワイルズのサポートに過去の教え子リチャード・テイラーがいました。彼とともに修正に挑みましたが、いよいよもうあと1か月で諦めようと振り返ったとき、ワイルズが途中でやめたアプローチである岩澤理論で、コリヴァギン・フラッハ法が補えることを閃きます。
そうして、ついにフェルマーの最終定理の証明が発表されることになるのです。
・『モジュラー楕円曲線とフェルマーの最終定理』アンドリュー・ワイルズ著
・『ある種のヘッケ環の環論的性質』リチャード・テイラー、アンドリュー・ワイルズ共著
8年に及んだ試練のなかで、ワイルズは20世紀の数論におけるほとんど全ての進歩を寄せ集め、絶大な力をもつ一つの照明に組み込んだ(中略)ワイルズの証明は、現代の数学と未来へのインスピレーションとの完璧なる統合なのである
『フェルマーの最終定理』p424
「フェルマーの最終定理」関連
パンサー尾形さんの『笑わない数学』
2022年にお笑いトリオ・パンサーの尾形さんがNHKで『笑わない数学』という番組のMC(?)に抜擢されて数学の難問にチャレンジしています。
尾形さんといえば、すっかり体当たり芸人というかドッキリ芸人というか、どこか愛らしく憎めない人ですよね。私は好きです(笑)。難問を解説してくれるような人ではなく、より私たちに近いところで難問にチャレンジする姿がかなり面白い。本人は「水曜日のダウンタウン」ではないかと疑ったそうですが…
この『笑わない数学』でフェルマーの最終定理が取り上げられてます。めっちゃお薦めですので、そちらもご覧いただくとよいかと思います!
●番組公式
笑わない数学(NHK)※NHK+でも配信中
●記事
パンサー尾形貴弘、NHK数学番組MCにドッキリ疑う 起用理由は「気の毒なほどの情熱」(ORICON NEWS 07-05)
まとめ
難解そうなわりに、物語として傑作の部類に入るのではないかという本作。文章で読む分には一気に読めてしまうほど読みやすく面白いのですが、いざまとめようと思うと時間がかかりましたね…笑 復習になってよかったです。
それにしても「フェルマーの最終定理」という、3世紀に渡るフェルマーへの挑戦がこれほどまでにどらまっチックなものだとは思いませんでした。解けない問題というのはまだまだ存在するようです(SF小説『三体』でも取り上げられた三体問題もその一つですかね)、過去の人物が「私は解けたけどね」とだけ残したものというのが、またくすぐられるものがありますよね。
そして、それがピタゴラスの定理をちょっと変えるだけだけという、数学の素人でも分かりやすい問題がこんなにも解けないというところが、フェルマーの最終定理の魅力だったんでしょう。
ところで、フェルマーの最終定理が解けることによって、どんな使い道があるのでしょうか。ちょっと調べてみたのですが分かりませんでした…これだとRPGクリア後のやり込みプレイみたいじゃないですか笑
本の目次
- 序 ジョナサン・リンチ
- はじめに サイモン・シン
- 第1章 「ここで終わりにしたいと思います」
- 1993年6月23日、ケンブリッジ
- 最終の問題
- 万物は数なり
- 完全無欠の証明
- 無数にある三つ組み数
- ピュタゴラスの定理からフェルマーの最終定理へ
- 第2章 謎をかける人
- 数論の発展
- 謎の誕生
- 余白のメモ
- フェルマーの最終定理、ついに出版される
- 第3章 数学の恥
- 数学のキュクロプス
- 遅々とした歩み
- ムッシュー・ル・ブラン
- 封印された手紙
- 第4章 抽象のなかへ
- パズルとクイズの時代
- 知識の基礎
- 好奇心に突き動かされて
- 力ずくの計算
- 大学院生
- 第5章 背理法
- 希望的観測
- 一人の大天才の死
- “良さの哲学”
- ミッシング・リンク
- 第6章 秘密の計算
- 屋根裏部屋の隠遁者
- 無限との闘い
- 最初のドミノ牌を倒す
- 「フェルマーの最終定理が解けた?」
- 闇の館
- コリヴァギン・フラッハ法
- 世紀の講演
- そして……
- 第7章 小さな問題点
- カーペット張り職人
- 悪夢の電子メール
- 誕生日の贈り物
- 第8章 数学の大統一
- 未解決の大問題
- シリコンによる証明
- 大切なもの
- 補遺
- 1 ピュタゴラスの定理の証明
- 2 √2が無理数であることに対するエウクレイデスの証明
- 3 ディオファントスの年齢の謎
- 4 バシェの分銅の問題
- 5 ピュタゴラスの三つ組み数が無限に存在することに対するエウクレイデスの証明
- 6 点予想の証明
- 7 不合理に迷い込む
- 8 算術の公理
- 9 ゲーム理論とトルエル
- 10 帰納法による証明の例



